Design Of Experiments

1.6 DESIGN OF EXPERIMENTS:

Experimental procedures in scientific and engineering applications are commonly guided by established laboratory procedures and protocols and are comparative in nature i.e. the experiments are mainly carried out primarily as a tool for comparison with an established process. The goal in any experimentation process is to characterize the relationship between response and a set of factors that influence the response. This can be achieved by conducting experiments and analyzing the data[10,11,13].

1.6.1 CONVENTATIONAL TECHNIQUE:

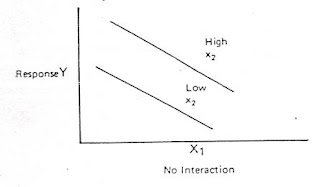
In a conventional experimentation technique, the experimental procedure was to hold all but one variable as constant while methodically changing one at a time. This is called one variable at a time technique or OVAT. When we obtain the better of the first factor, we will start varying the other variables at that best level. This is well and good if there is no influence of combined factors in the response of the experiment. Therefore, the conventional experimentation procedure is a failure when there is the influence of combined factor effects on the response. If there are three factors X₁, X₂, X₃ that have been identified as influencing the outcome of the experiment, then in an OVAT in the first step X₁, X₂ are held constant and the experiment is carried out by changing X₃. From the experimental data obtained, the best of X₃ is found (X_3b). In the second step, experimental procedure is carried out by changing X₂, by keeping X₁ constant at best X_3b. This gives the best value of X₂ (X_2b). Then in the final step the value of X₁ is optimized by keeping X_2b and X_3b constant. Thus the best value of X₁ (X_1b) is obtained. The major fallout of this method is that the best value of these variables is not the best of all i.e. the value of X₁ is best only at the fixed values of X_2b and X_3b. The interaction effect of two or more factors can be explained using the figures given below[4,10,].

Fig.1.8 Levels of Interaction Between X1 and X2

The other major pitfall of this OVAT process is that the experimenter will not consider the joint effects of the variables on the out come. Therefore, the need of statistical design of experimentation is very essential in situations where the combined factor effects have considerable influence on the outcome of an experiment. The main advantages of statistical design are:

· It generates relatively accurate data with minimum number of experiments thereby saving valuable materials and time.

· Ability to evaluate factor effects mathematically.

· It covers a large experimental region with minimum number of experiments.

1.6.2 TYPES OF STATISTICAL DESIGN:

The statistical designs include Factorial Designs, Central Composite Design, Box – Behnken Design and the Taguchi Method. These designs require coding levels for the variables. Coding helps in dealing with different factors on similar terms i.e. the experimental design units or the coded levels[13,19].

TYPES OF STATISTICAL DESIGNS:

FACTORIAL AND FRACTIONAL DESIGNS:

When the investigator selects two levels for each of a number of variables (k factors) and runs the experiments with all possible combinations, it is referred to as a 2^k factorial design. The number of runs required by a full 2^k factorial design increase geometrically as k is increased. It turns out, however, that when k is not small the desired information can often be obtained by performing only a fraction of the full factorial design called as fractional factorial designs. Typical design tables for two- factor and three-factor experiment is given below:

Fig.1.9 Design Table for Two Factor Factorial Design

Trial no.	X1	X2
1.	-1	-1
2.	-1	+1
3.	+1	-1
4.	+1	+1

Fig.1.10 Design Table for Three Factor Factorial Design

Trial no.	X1	X2	X3
1.	-1	-1	-1
2.	+1	-1	-1
3.	-1	+1	-1
4.	+1	+1	-1
5.	-1	-1	+1
6.	+1	-1	+1
7.	-1	+1	+1
8.	+1	+1	+1

CENTRAL COMPOSITE DESIGN:

CCD is a rotatable design that provides equal precision for fitted response at points (factor level combinations) that are equal distances from the centre of the factor space. The CCD is a rotatable design which would require 5 levels of each factor (-a, -1, 0, +1, +a).

BOX – BEHNKEN DESIGN:

Unlike the CCD, which employs five levels of each factor, Box – Behnken designs enable use of minimum number of levels. This system uses a subset of points in the corresponding full three - level factorial. The design table for three variable Box – Behnken method is given in fig 1.10

Fig.1.11Design Table for Three-Factor Box – Behnken Design

Trial no.	X1	X2	X3
1.	+1	+1	0
2.	+1	-1	0
3.	-1	+1	0
4.	-1	-1	0
5.	+1	0	+1
6.	+1	0	-1
7.	-1	0	+1
8.	-1	0	-1
9.	0	+1	+1
10.	0	+1	-1
11.	0	-1	-1
12.	0	-1	+1
13.	0	0	0
14.	0	0	0
15.	0	0	0
16.	0	0	0

TAGUCHI METHOD ( ROBUST DESIGN):

Dr. Taguchi of Japan has developed a method based on “ORTHOGONAL ARRAY” experiments, which gives much-reduced “variance” for the experiment with “optimum settings” of control parameters.

Taguchi method is an engineering methodology to improve the quality of process / product. It focuses on minimizing the variance rather than realizing a desired mean value. It is achieved by planning and conducting matrix experiments using orthogonal arrays, which provide a minimum set of experiments needed for the prediction of optimum settings of control parameters.

The goal of quality improvement effort can be stated as attempting to maximize the signal to noise ratio for the respective product. The S/N ratios have been proposed by Taguchi for common (static) engineering problems. Signal factors are those factors that are set or control by the operator of the product to make use of its intended functions. Noise factors are those that are not under the control of the operator of a product.

Thus, the combination of Design of Experiments with optimization of control parameters to obtain BEST results is achieved in the Taguchi Method. "Orthogonal Arrays" (OA) provide a set of well-balanced (minimum) experiments.

Orthogonal array

Orthogonal Arrays are special experimental designs that require only a small no of trials to help discover main factors. It is nothing but a fractional factorial matrix, which assures balanced comparison of levels of any factor or interaction of factors. It is a matrix of numbers arranged in rows and columns. In orthogonal array, columns are mutually orthogonal. That is, for any pair of columns all combination of factor levels occurs and they occur an equal number of times. The number of columns of an orthogonal array represents the maximum number of factors that can be studied using that array. The

· Orthogonal array specified by Taguchi has certain standard arrays.

Ø Some of the standard orthogonal arrays are

L₄(2³) : 4 experiments, 2 levels and 3 columns

L₈(2⁷) : 8 experiments, 2 levels and 7 columns

L₁₈(2¹*3⁷) : 18 experiments, 3levels and 8 columns

METHODOLOGY:

Step 1 : Reduce the variation irrespective of the target value.

Step 2 : Adjust the performance on target leaving the variation undisturbed.

SIGNAL TO NOISE RATIO:

In the field of Communication Engineering, a quantity called the signal – to – noise ratio (SN) ratio has been used as the quality characteristic of choice. Taguchi whose background is electronics has introduced the same concept in the Designof Experiments. Thus, he used the term noise (corresponding to uncontrollable factor) and the term signal (corresponding to controllable factor)[13].

The S – N ratio transforms several repetitions into one value, which reflects the amount of variation present and the mean response.

S – N ratio =( power of signal / power of noise) ; µ / σ²

1.6.3 ANALYSIS OF DATA:

The data obtained from any experiment is used to draw inferences on the phenomena or the processes under investigation. A statistically designed experiment is usually conducted with the intent of better understanding populations, observable phenomena and stable processes. Therefore, the need arises of relating the response to the factors. If two factors are varied then the effect of both the factors on the response should be quantitatively measured.

Most engineering experiments are conducted to not only obtain data but also fit some type of mathematical equations and find the validity of use of these equations for further factor levels. Usually three types of mathematical fits are used they are:

Least square fit

Polynomial fit

Regression analysis

1.6.4 ANALYSIS OF VARIANCE:

Analysis of variance takes the total variation in the response and determines how much this variation is accounted for by the equation. The variation not accounted for by the equation is divided into variation due to model inadequacy and variation due to experimental error. For the response, equations to fit adequately, the F_model should be significant and F_{lack of fit} should be 10 – 15 times greater than that required for bare significance level.

The Coefficient of Determination, R – Square Test:

The coefficient of determination, R², is another extensively used measure of the goodness of fit of a regression model. It is equal to the amount of variation of the response accounted by the equation divided by the total variation in the response. In short R² * 100 is the % of total variation in the response which the equation explains

R² = 1 – ( SSE / TSS )

For least squares estimates of the model parameters, the value of R² lies between 0 & 1; the closer it is to 1 the closer the predicted responses are to be observed.

The coefficient of determination is often adjusted to take account of the number of observations and the number of predictor variables. This adjustment is made because R² can be arbitrarily close to 1 if the number of predictor variables is too close to the number of observations. The adjusted R² is calculated from the formula

R_a² = 1 * a* (SSE / TSS)

where a = n/(n- p); TSS – total sum of squares.