3.4.5 WATER ABSORPTION (ASTM D 570)

3.4.5 WATER ABSORPTION (ASTM D 570):

The water absorption test was carried out as per the procedure explained in the chapter 2. The results are tabulated as shown in the table 3.18. From the results obtained, we can infer that the water absorption of the calcium carbonate filled HDPE is almost equal to zero percentage.

Table 3.18 Results of water absorption test for calcium carbonate-HDPE system.

TRIAL	X1	X2	INITIAL WEIGHT, (g)	FINAL WEIGHT, (g)	WATER ABSORPTION %
1	60	5	7.604	7.606	2*10-4
2	60	25	8.532	8.532	0
3	80	5	7.666	7.676	1.3*10-3
4	80	25	5.460	5.461	1.8*10-4
5	56	15	7.729	7.731	2.5*10-4
6	84	15	8.144	8.145	1.2*10-4
7	70	1	7.53	7.53	0
8	70	29	8.559	8.561	2.3*10-4
9	70	15	8.192	8.196	4.8*10-4
10	70	15	8.192	8.196	4.8*10-4
11	70	15	8.192	8.196	4.8*10-4

4.0 CONCLUSION

An attempt has been made to optimize the amount of filler loading in the HDPE matrix in order to get the desired properties at a comparatively low cost. The optimum mixture is going to be used in the manufacture of blow-molded articles.

The factors, which affect the properties of the filled formulation, were identified and a suitable design of experiments was selected to carry out the study in order to minimize the number of trials, to compensate for the interaction effects of the factors and to obtain maximum information from minimum number of experiments. Response Surface Methodology was applied to the filler optimization.

Compounding trials were carried out at the design points as given in the table and the resultant compound was characterized for mechanical properties such as Tensile Strength, Youngs Modulus, Hardness, Impact Strength, Flexural strength and water absorption. The data obtained from the characterization were used to generate models by linear regression analysis using MINITAB and MATLAB packages. The effect of each factor on the response was tested at 5% level of significance.

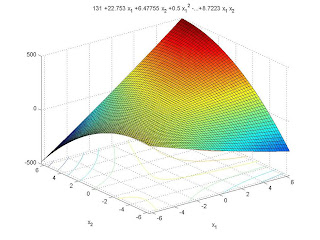
From the tensile strength data linear regression analysis was performed and the following equation was generated

Y = 130.882+ 22.891X₁ +6.515X₂ -4.69X₁² +8.958X₂² +0.5X₁ X₂.

In the above equation the coefficients of X₁, X₂, X₂² are positive and these have a positive effect on the property i.e. the increase in the value of X₁, X₂, X₂² results in a subsequent increase of the property. Though the interaction effect of X₁ X₂ is present, it is very low when compared to the other coefficients. The coefficient of X₁² is negative and it has a negative effect on the property. Using the regression equation, the contour diagrams were generated. A rising ridge type of contour was obtained in which the best ranges for X1 and X2 were found to be 65 – 85 and 0 – 25 respectively.

From the Youngs Modulus data, linear regression analysis was performed and the following equation was generated.

In the above equation only the co –efficient of X1 is positive and this has a positive effect on the property i.e. the increase in the value of X1 results in a subsequent increase of the property. The interaction effect of X₁ X₂ is also present, it has a negative effect on the property, but it is very low when compared to the other coefficients. The coefficients of other factors are negative and they have a negative effect on the property.

Using the regression equation contour diagrams and response surfaces are generated. A contour diagram of the property vs. factor X1 was generated in which the best value of X1 was found to be between 70 & 75.

From the Percentage Elongation at break data, linear regression analysis was performed and the following equation was generated.

In the above equation the coefficients of all the factors are positive. Hence, all the factors have a positive influence on the Percentage Elongation. Using the regression equation contour diagrams and response surfaces are generated. A stationary ridge type contour diagram was obtained in which the best range for X1 and X2 was found to be between 75 & 85 and 20 & 30 respectively.

From the Flexural Modulus data, linear regression analysis was performed and the following equation was generated.

In the above equation the coefficients of X1 and X2 are positive and these have a positive effect on the property i.e. the increase in the value of X1 results in a subsequent increase of the property. The interaction factor X₁ X₂, X₁² and X₂² have a negative effect on the Flexural Modulus. The interaction parameter has a more pronounced effect on the Flexural Modulus. Using the regression equation contour diagrams and response surfaces are generated. A mound shaped contour diagram was obtained in which the best ranges of X1 and X2 were found to be between 65 & 80 and 10 & 20 respectively.

From the Flexural strength data, linear regression analysis was performed and the following equation was generated.

In the above equation the coefficients of X1 and X2 are positive and these have a positive effect on the property i.e. the increase in the value of X1 results in a subsequent increase of the property. The interaction factor X₁ X₂, X₁² and X₂² have a negative effect on the Flexural strength. Using the regression equation contour diagrams and response surfaces are generated. A saddle type contour diagram was obtained in which the best ranges of X1 and X2 were found to be between 55 & 63 and 22 & 30 and 0 &15 and 75 & 85 respectively.

From the Shore – A Hardness data, linear regression analysis was performed and the following equation was generated.

In the above equation the coefficients of all the factors were found to be negative and hence all the factors have a negative influence on the hardness. Using the regression equation contour diagrams and response surfaces are generated. A rising ridge shaped contour diagram was obtained in which the best ranges of X1 and X2 were found to be between 68 & 80 and 10 & 20 respectively.

From the Shore – D Hardness data, linear regression analysis was performed and the following equation was generated.

In the above equation the coefficients of all the factors except that one of X2 were found to be negative. Hence, only the factor X2 has a positive influence on the Hardness and all the other factors have a negative influence on the Hardness. Using the regression equation contour diagrams and response surfaces are generated. A rising ridge shaped contour diagram was obtained in which the best ranges of X1 and X2 were found to be between 55 & 68 and 18 & 25 respectively.

From the Charpy Impact data, linear regression analysis was performed and the following equation was generated.

In the above equation, the coefficients of X₁, X₁² and X₁X₂ factors were found to be positive and hence all these factors have a positive influence on the Impact. The coefficients of the other terms were negative and hence they have negative effect on the Impact strength. Using the regression equation contour diagrams and response surfaces are generated. A saddle type contour diagram was obtained in which the best ranges of X1 and X2 were found to be between 75 & 85 and 22 & 30 respectively.

From the Izod Impact data, linear regression analysis was performed and the following equation was generated.

In the above equation, the coefficients of X₁, X₁², X₂² and X₁X₂ factors were found to be positive and hence all these factors have a positive influence on the Impact. The coefficients of the other terms were negative and hence they have negative effect on the Impact strength. Using the regression equation contour diagrams and response surfaces are generated. A saddle type contour diagram was obtained in which the best ranges of X1 and X2 were found to be between 77 & 85 and 25 & 30 respectively.

From the Percentage Elongation at peak data, linear regression analysis was performed and the following equation was generated.

In the above equation, the coefficients of X₁, X₂, X₁ X₂ factors are positive. Hence, all these factors have a positive influence on the Percentage Elongation at peak. The coefficients of all the other factors are negative and hence they have a negative effect on the elongation. Using the regression equation contour diagrams and response surfaces are generated. A contour diagram vs. the factor X₁ generated and the best value of the X₁ was found to be between 60 & 65.

The equations and diagrams that are generated using MINITAB can be used with an accuracy of 90 % in all cases.

The contour plots obtained individual properties were overlaid to overlaid contour plots in order to get simultaneous optimization of the various properties of interest. The contour plots of all the Tensile properties (Tensile strength, Youngs Modulus, and Percentage Elongation at break) were optimized simultaneously and it was found that the desired properties could be obtained at any combination in the white coloured region of the plot.

The individual contour plots of the Flexural properties (Flexural Modulus, Flexural strength, and Percentage Elongation @ peak ) were also overlaid and from the over laid contour plot it was found that the desired properties could be obtained at any combination within the optimized region indicated by the white coloured region in the contour plot.

3.4.4 HARDNESS (ASTM D 2240)

3.4.4 HARDNESS (ASTM D 2240):

SHORE – A:

The Shore – A Hardness test was performed as per the procedure explained in the chapter 2 and the results were tabulated as shown in table 3.15. From the results, regression analysis had been performed to get the regression equation, which is shown in the table 3.16. Then using the equation contour plots and response surfaces are generated which are shown in fig 3.21 and 3.22. The desired values of

Shore – A Hardness can be obtained at any combination within the optimized region as indicated in the contour plot. The value of X1 varies from 68 – 82 and X2 varies from 10 – 20 in the optimum region.

SHORE – D:

The Shore – A Hardness test was performed as per the procedure explained in the chapter 2 and the results were tabulated as shown in table 3.15. From the results, regression analysis had been performed to get the regression equation, which is shown in the table 3.17. Then using the equation contour plots and response surfaces are generated which are shown in fig 3.23 and 3.24. The desired values of

Shore – D Hardness can be obtained at any combination within the optimized region as indicated in the contour plot. The value of X1 varies from 55 - 67 and X2 17 - 25 varies from in the optimum region.

Table 3.15 Results of Shore – A and Shore – D Hardness tests for CaCO₃ – HDPE system:

TRIAL	X1	X2	SHORE – A HARDNESS	SHORE – D HARDNESS
1	60	5	76	54.3
2	60	25	79.0	56.0
3	80	5	81.0	58.3
4	80	25	78.3	56.3
5	56	15	78.3	59.0
6	84	15	80.3	58.0
7	70	1	78.0	57.3
8	70	29	80.6	57.3
9	70	15	81.0	57.6
10	70	15	81.0	57.6
11	70	15	81.0	57.6

Table 3.16 Estimated Regression Coefficients for Hardness- Shore A

Term	Coef	SE Coef	T	P
Constant	81.0095	0.4285	189.037	0.000
X1	0.9003	0.2638	3.413	0.019
X2	0.5119	0.2638	1.940	0.110
X1*X1	-1.0388	0.3166	-3.281	0.022
X2*X2	-1.0388	0.3166	-3.281	0.022
X1*X2	-1.4175	0.3712	-3.819	0.012

S = 0.7424 R-Sq = 90.3% R-Sq (adj) = 80.7%

The regression equation is

Y = 81.0095 +0.9003X₁ +0.5119X₂ -1.0388X₁² -1.0388X₂² -1.4175X₁ X₂.

Table 3.17 Estimated Regression Coefficients for Hardness- Shore D

Term	Coef	SE Coef	T	P
Constant	57.6223	0.8001	72.015	0.000
X1	0.3699	0.4925	0.751	0.486
X2	-0.0417	0.4925	-0.085	0.936
X1*X1	0.0210	0.5912	0.035	0.973
X2*X2	-0.5760	0.5912	-0.974	0.375
X1*X2	-0.9175	0.6930	-1.324	0.243

S = 1.386 R-Sq = 40.3% R-Sq (adj) = 0.0%

The regression equation is

Y = 57.6223 +0.3699X₁ -0.0417X₂ +0.0210X₁² -0.576X₂² -0.9175X₁ X₂.

Fig. 3.21 Contour Plot of Hardness – Shore A vs. X1, X2

Fig. 3.22 Response surface of Hardness – Shore A vs. X1, X2

Fig. 3.23 Contour plot of Hardness – Shore D vs. X1, X2

Fig. 3.24 Response surface of Hardness – Shore D vs. X1, X2

OVERLAYING OF CONTOUR PLOTS:

The individual contour plots were generated for each of the property and then simultaneous optimization of properties were carried out by overlaying the individual plots to obtain the overlaid contour plots.

The desired values of all these properties can be obtained at any given combination within the optimized region indicated by the white coloured region in the fig.3.20. The values of both X1 and X2 vary over a wide range in the optimized region.

The desired values of all these properties can be obtained at any given combination within the optimized region indicated by the white coloured region in the fig.3.13. The value of X1 varies from 77 – 80 and X2 varies from 5 – 17 in the optimized region.

Fig. 3.20 Overlaid Contour plot of Tensile Properties

Fig. 3.13 Overlaid contour Plot of Flexural Properties

3.4.3 TENSILE PROPERTIES (ASTM D-638)

3.4.3 TENSILE PROPERTIES (ASTM D-638):

The tensile strength test was performed as per the procedure explained in the chapter 2 and the results were tabulated as shown in table 3.11. The properties that were evaluated as a part of tensile strength test are tensile strength at break load, percentage elongation at break load and Youngs modulus. From the results, regression analysis had been performed to get the regression equations, which are shown in the tables 3.12, 3.13, 3.14. Then using the equations contour plots and response surfaces were generated for each of them as shown in the figures 3.14 – 3.19.

Table 3.11 Results of Tensile Properties for CaCO₃ – HDPE system

Trial no.	X1	X2	Youngs modulus (kg/cm2 )	Tensile strength @ break load (kg/cm2 )	Percentage elongation @ break load
1.	60	5	1214	104	80.2
2.	60	25	1157	119	66.5
3.	80	5	1337	159	90.5
4.	80	25	1205	176	174
5.	56	15	840	92.5	66.4
6.	84	15	1113	142	193
7.	70	1	1318	137	52
8.	70	29	1135	151	87
9.	70	15	1297	131	68.6
10.	70	15	1297	131	68.6
11.	70	15	1297	131	68.6

Table 3.12 Estimated Regression Coefficients for Tensile Strength @ break load

Term	Coef	SE Coef	T	P
Constant	130.882	5.054	25.895	0.000
X1	22.891	3.111	7.358	0.001
X2	6.515	3.111	2.094	0.090
X1*X1	-4.690	3.735	-1.256	0.265
X2*X2	8.958	3.735	2.399	0.062
X1*X2	0.500	4.378	0.114	0.914

S = 89.52 R-Sq = 80.4% R-Sq (adj) = 60.8%

The regression equation is

Y = 130.882+ 22.891X₁ +6.515X₂ -4.69X₁² +8.958X₂² +0.5X₁ X₂.

Table 3.13 Estimated Regression Coefficients for Tensile Strength Youngs Modulus

Term	Coef	SE Coef	T	P
Constant	1295.26	51.68	25.064	0.000
X1	69.85	31.81	2.196	0.080
X2	-56.21	31.81	-1.767	0.137
X1*X1	-129.30	38.18	-3.386	0.020
X2*X2	-1.74	38.18	-0.046	0.965
X1*X2	-18.75	44.76	-0.419	0.693

S = 89.52 R-Sq = 80.4% R-Sq (adj) = 60.8%

The regression equation is

Y = 1295.26+ 69.85X₁ -56.21X₂ -129.3X₁² -1.74X₂² -18.75X₁ X₂.

Table 3.14 Estimated Regression Coefficients for Percentage Elongation

Term	Coef	SE Coef	T	P
Constant	68.566	6.073	11.290	0
X1	37.253	3.738	9.965	0
X2	15	3.738	4.012	0.01
X1*X1	31.846	4.488	7.096	0.001
X2*X2	1.131	4.488	0.252	0.811
X1*X2	24.3	5.260	4.619	0.006

S = 10.52 R-Sq = 97.41% R-Sq (adj) = 94.9%

The regression equation is

Y = 68.566+ 37.253X₁ +15X₂ +31.846X₁² +1.131X₂² +24.3X₁ X₂.

Fig. 3.14 Contour Plot of tensile strength at break load vs. X2, X1

Fig. 3.15 Response surface of tensile strength at break load vs. X2, X1

Fig. 3.16 Plot of Youngs Modulus vs. X1

Fig. 3.17 Response surface of Youngs Modulus vs. X2, X1

Fig. 3.18 Contour plot of Percentage Elongation vs. X2, X1

Fig. 3.19 Response surface of Percentage Elongation vs. X2, X1